問題１#

位相回転するゲートは？#

  1. Xゲート

  2. Yゲート

  3. Zゲート

  4. Tゲート

  5. Sゲート

答えはこちら Z軸の周りを回転することを位相回転（Phase flip）という

  1. Zゲート

  2. Tゲート

  3. ゲート

問題２#

ビット反転するゲートは？#

  1. Xゲート

  2. Zゲート

  3. Tゲート

  4. Sゲート

答えはこちら パウリX行列をつかうと|0>が|1>に|1>が|0>になる。これをビット反転（bit flip）という.

  1. Xゲート

問題３#

下記を実行すると、量子状態はどうなりますか1？#

問題画像

答えはこちら アダマールゲートのあとCCXゲートを通している事を確認してください

Bell状態になります

問題４#

下記を実行すると、量子状態はどうなりますか2？#

問題画像

答えはこちら

GHZ状態になります

問題５#

下記と等価なゲートは1？#

問題画像

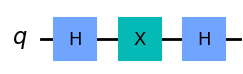
答えはこちら 図と同じゲートはZゲートになります

問題６#

下記と等価なゲートは2？#

問題画像

答えはこちら 図と同じゲートはXゲートになります

問題７#

Sゲートのフェーズの値は？#

  1. π/2

  2. π/4

  3. π/8

  4. π

答えはこちら 1. π/2

問題８#

Tゲートのフェーズの値は？#

  1. π/2

  2. π/4

  3. π/8

  4. π

答えはこちら 2. π/4

問題９#

QuantumCircuit　正しくない記述は？#

  1. QuantumCircuit(QuantumRegister(4))

  2. QuantumCircuit(QuantumRegister(4), ClassicalRegister(3))

  3. QuantumCircuit(QuantumRegister(4, ‘qr0’), QuantumRegister(2, ‘qr1’))

  4. QuantumCircuit（4,4)

  5. QuantumCircuit（cr,qr)

  6. qr = QuantumRegister(2)
    cr = ClassicalRegister(2)
    qc = QuantumCircuit(cr[0:2],qr[0:2])

答えはこちら すべて正しい記述です。

問題10#

Measure　正しくない記述は？#

  1. circuit = QuantumCircuit(2, 2)
    circuit.measure([0,1], [0,1])

  2. circuit = QuantumCircuit(2, 2)
    circuit.measure(0, 0)
    circuit.measure(1, 1)

  3. qreg = QuantumRegister(2, “qreg”)
    creg = ClassicalRegister(2, “creg”)
    circuit = QuantumCircuit(qreg, creg)
    circuit.measure(qreg, creg)

  4. circuit = QuantumCircuit(qreg, creg)
    circuit.measure(qreg[0], creg[0])

答えはこちら

回答作成中です

問題11#

plot_histogram()のオプションで、ラベルを追加するのは？#

  1. legend

  2. short

  3. number_to_keep

  4. bar_labels

答えはこちら ラベルは1.legendオプションで追加します。
ラベルに表記する文字は、リストとして渡す必要があります。

問題画像

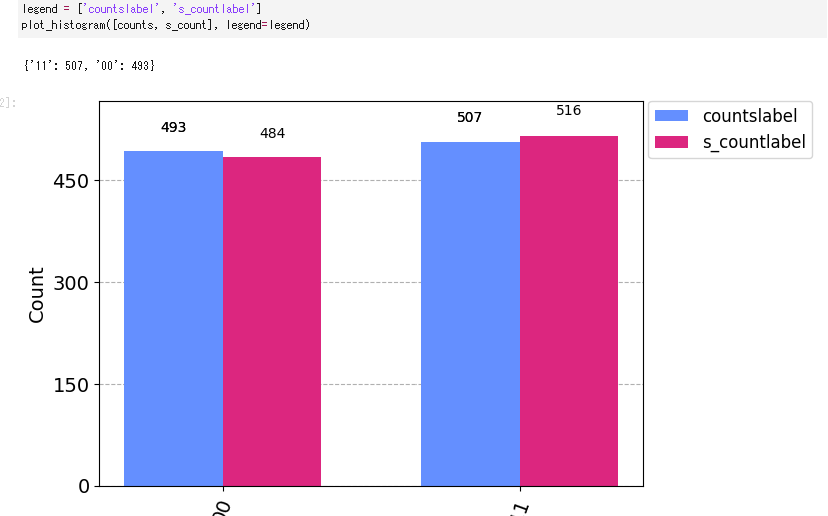
問題12#

plot_histogram()のオプションで、バーの色を変更するのは？#

  1. legend

  2. color

  3. number_to_keep

  4. bar_labels

答えはこちら ラベルは2.colorオプションで変更します。

問題13#

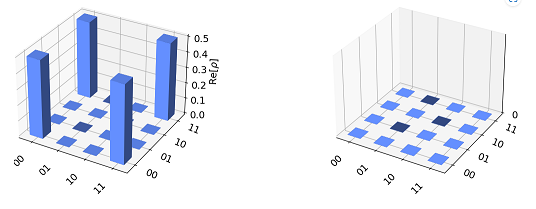
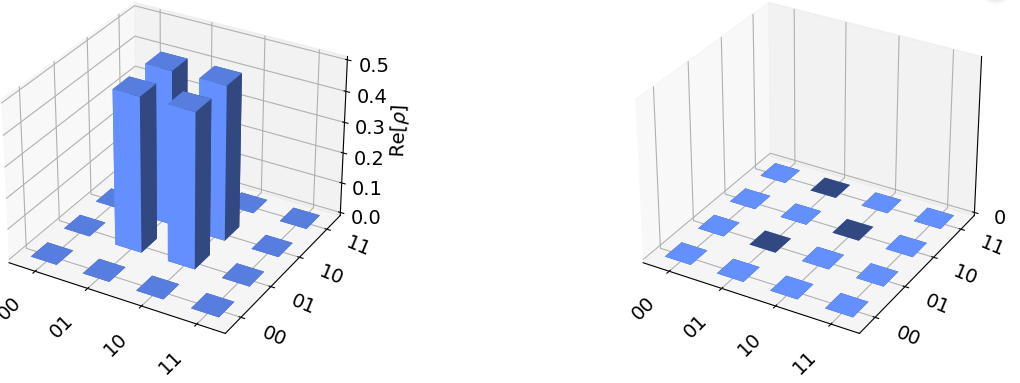
以下のコードで出力されるのはどちらですか？#

qc = QuantumCircuit(2)
qc.h(0)
qc.cx(0, 1)

state = DensityMatrix(qc)
plot_state_city(state)


  1. 問題画像


  2. 問題画像

答えはこちら

1.が正解です。bell状態をplot_state_cityで表示したものです。 2,は
qc.h(0)
qc.x(0)
qc.cx(0, 1)
の状態です
plot_state_cityは状態行列の実部と虚部が都市のようにプロットされている、量子状態の標準的なビュー。

問題14#

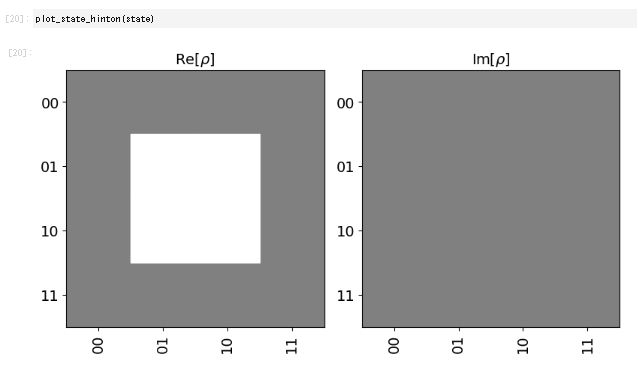
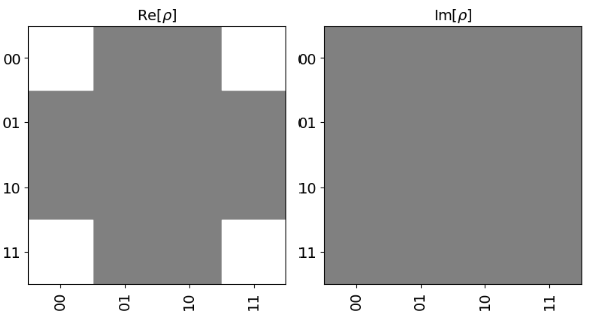
以下のコードで出力されるのはどちらですか？#

qc = QuantumCircuit(2)
qc.h(0)
qc.cx(0, 1)

state = DensityMatrix(qc)
plot_state_hinton(state)


  1. 問題画像


  2. 問題画像

答えはこちら 1.が正解です。bell状態をplot_state_cityで表示したものです。 2,は
qc.h(0)
qc.x(0)
qc.cx(0, 1)
の状態です

問題15#

下記のコードで出力されるのは？#

Importing standard Qiskit libraries from qiskit.quantum_info import random_statevector, random_unita

random_statevector(2)

  1. Operator([[ 0.74182434-0.14258211j, 0.03447796+0.65435332j], [ 0.13139464-0.64195206j, -0.71237596-0.25130361j]], input_dims=(2,), output_dims=(2,))

  2. Statevector([ 0.13919545-0.10896992j, -0.24642315-0.95290389j], dims=(2,))

  3. Statevector([ 0.22981074-0.11260163j, -0.42290579+0.31550685j, 0.46396693+0.58555583j, -0.21718184-0.22539993j], dims=(2, 2))

  4. Operator([[ 0.74182434-0.14258211j, 0.03447796+0.65435332j], [ 0.13139464-0.64195206j, -0.71237596-0.25130361j]], input_dims=(2,), output_dims=(2,))

答えはこちら

2．が正解です。

問題16 下記のコードで出力されるのは？#

Importing standard Qiskit libraries from qiskit.quantum_info import random_statevector, random_unita

random_unitary(2)

  1. Operator([[ 0.74182434-0.14258211j, 0.03447796+0.65435332j], [ 0.13139464-0.64195206j, -0.71237596-0.25130361j]], input_dims=(2,), output_dims=(2,))

  2. Statevector([ 0.13919545-0.10896992j, -0.24642315-0.95290389j], dims=(2,))

  3. Statevector([ 0.22981074-0.11260163j, -0.42290579+0.31550685j, 0.46396693+0.58555583j, -0.21718184-0.22539993j], dims=(2, 2))

  4. Operator([[ 0.74182434-0.14258211j, 0.03447796+0.65435332j], [ 0.13139464-0.64195206j, -0.71237596-0.25130361j]], input_dims=(2,), output_dims=(2,))

答えはこちら

1．が正解です。

–

問題17#

下記のコードでDepthはいくつになりますか？#

qc = QuantumCircuit(3,3)
qc.x(0)
qc.ccx(0,1,2)
qc.h(2)
qc.ccx(0, 1, 2)
qc.h(0)
qc.depth()

  1. 4

  2. 5

  3. 6

  4. 7

答えはこちら Depthは5です。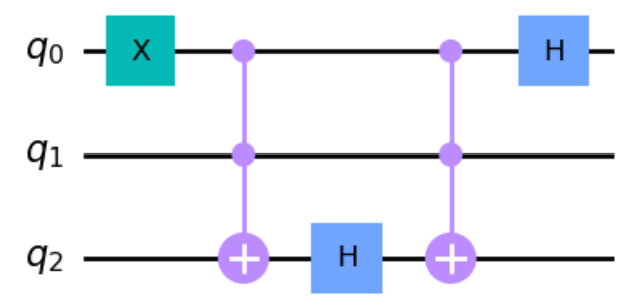

問題画像

–

問題18#

下記のコードでDepthはいくつになりますか？#

qc = QuantumCircuit(3,3)
qc.x(0)
qc.h(2)
qc.ccx(0,1,2)
qc.ccx(0, 1, 2)
qc.h(0)
qc.depth()

  1. 4

  2. 5

  3. 6

  4. 7

答えはこちら Depthは4です。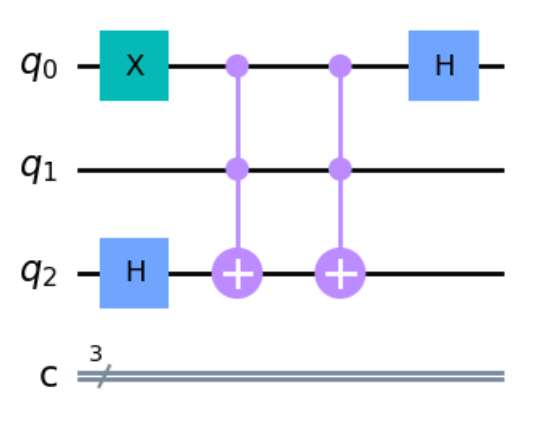

問題画像

問題19#

下記が表示されるコードは？#

問題画像


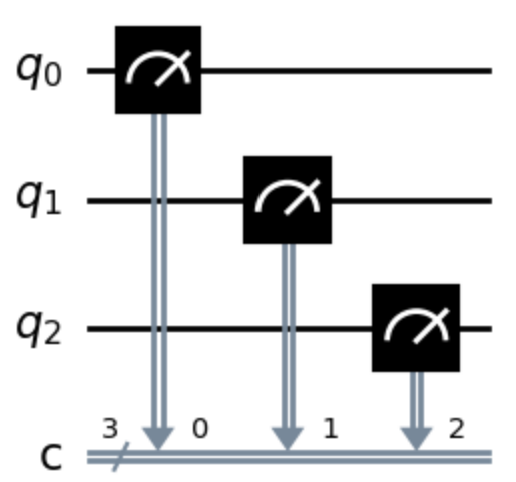
qc = QuantumCircuit(3,3)
qc.measure(0,0)
qc.measure(1,1)
qc.measure(2,2)
2.
qc = QuantumCircuit(3,3)
qc.measure([0,1,2],[0,1,2])
3.
qc = QuantumCircuit(3,3)
qc.measure_all()
4.
qr = QuantumRegister(3, ‘q’)
cr = ClassicalRegister(3, ‘c’)
qc = QuantumCircuit(qr, cr)
qc.measure(qr, cr)

答えはこちら

3.が不正解。ほかの選択肢は全て正解。
mesure_allを利用すると、下記になります

問題画像

問題20#

下記のコードで得られる図形は？#

num_qbits = 5
coupling_map=[[0,1],[1,2],[1,3],[3,4]]
qbit_coordinates=[[1,0],[0,1],[1,1],[1,2],[2,1]]
plot_coupling_map(num_qbits,qbit_coordinates,coupling_map)


問題画像


問題画像


問題画像


問題画像

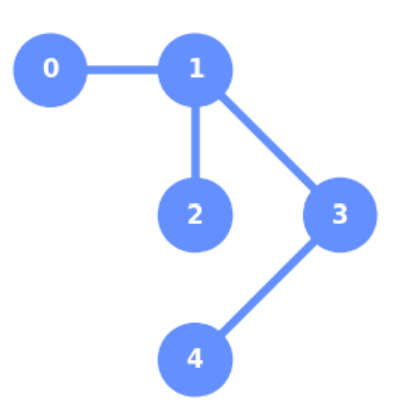
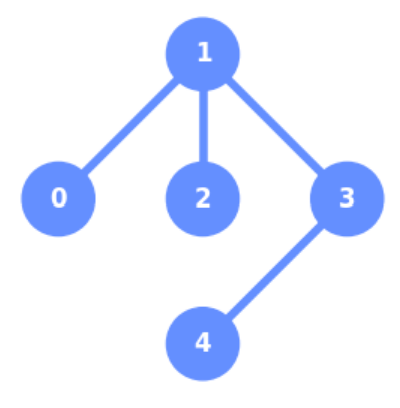
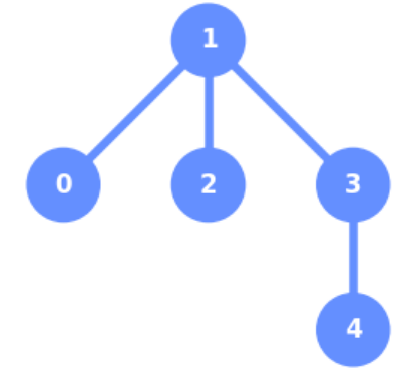
答えはこちら

3.が正解
coupling_mapはビット同士のつながりを示す。
qbit_coordinatesは、０から始まる平面座標上のどこにあるかを示す。
qbit_coordinates=[[1,0],[0,1],[1,1],[1,2],[2,1]]
0ビットは[1,0]で、縦方向に1、横方向に0
1ビットは[0,1]で、縦方向に0、横方向に1
2ビットは[1,1]で、縦方向に1、横方向に1
3ビットは[1,2]で、縦方向に1、横方向に2
4ビットは[2,1]で、縦方向に2、横方向に1
問題画像

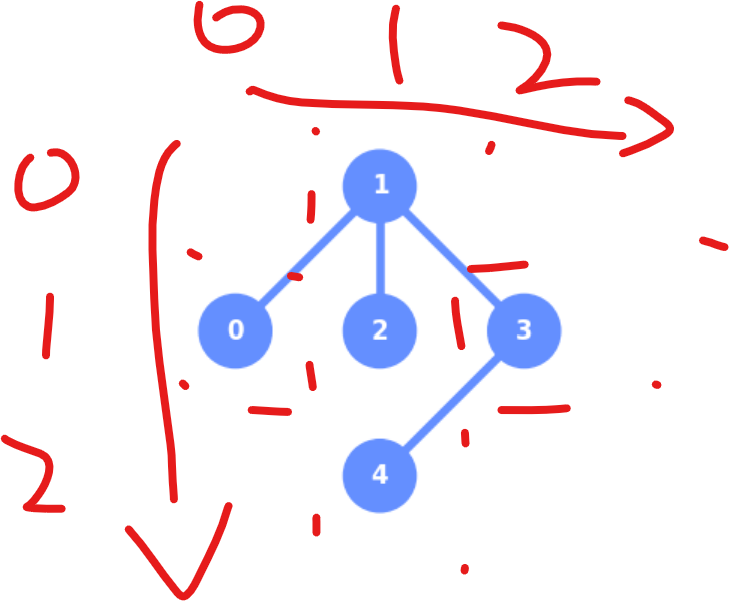
問題21#

下記コードの値は？#

qc = QuantumCircuit(2)
qc.cx(0,1)
qc.measure_all()
qc.draw()

  1. {‘00’: 1024}

  2. {‘01’: 1024}

  3. {‘10’: 1024}

  4. {‘11’: 1024}

答えはこちら

  1. {‘00’: 1024}

問題22#

下記コードの値は？#

qc = QuantumCircuit(2)
qc.x(0)
qc.measure_all()
qc.draw()

  1. {‘00’: 1024}

  2. {‘01’: 1024}

  3. {‘10’: 1024}

  4. {‘11’: 1024}

答えはこちら

  1. {‘01’: 1024}

問題23#

下記コードの値は？#

qc = QuantumCircuit(3)
qc.ccx(0,1,2)
qc.measure_all()
qc.draw()

  1. {‘000’: 1024}

  2. {‘001’: 1024}

  3. {‘100’: 1024}

  4. {‘111’: 1024}

答えはこちら

  1. {‘000’: 1024}

問題24#

下記コードの値は？#

qc = QuantumCircuit(3)
qc.x(0)
qc.ccx(0,1,2)
qc.measure_all()
qc.draw()

  1. {‘000’: 1024}

  2. {‘001’: 1024}

  3. {‘100’: 1024}

  4. {‘111’: 1024}

答えはこちら

  1. {‘001’: 1024}

問題25#

下記コードの値は？#

qc = QuantumCircuit(3)
qc.x(0)
qc.x(1)
qc.ccx(0,1,2)
qc.measure_all()
qc.draw()

  1. {‘000’: 1024}

  2. {‘001’: 1024}

  3. {‘100’: 1024}

  4. {‘111’: 1024}

答えはこちら

  1. {‘111’: 1024}

問題26#

以下の結果が表示されるコードは？#

qc = QuantumCircuit(2)

qc.h(0)
qc.cx(0,1)

#insert code 下記選択しから選んでください

問題画像

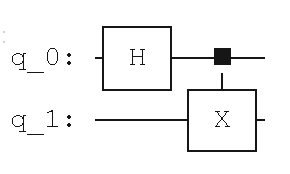
  1. qc.draw(‘mpl’)

  2. qc.draw(‘text’)

  3. print(qc)

  4. qc.draw(‘latex_source’)

答えはこちら

  1. qc.draw(‘text’)

問題27#

以下の結果が表示されるコードは？#

qc = QuantumCircuit(2)

qc.h(0)
qc.cx(0,1)

#insert code 下記選択しから選んでください

問題画像

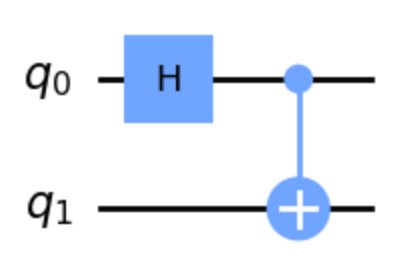
  1. qc.draw(‘mpl’)

  2. qc.draw(‘text’)

  3. print(qc)

  4. qc.draw(‘latex_source’)

答えはこちら

  1. qc.draw(‘mpl’)

問題28#

以下の結果が表示されるコードは？#

qc = QuantumCircuit(2)

qc.h(0)
qc.cx(0,1)

#insert code 下記選択しから選んでください

問題画像

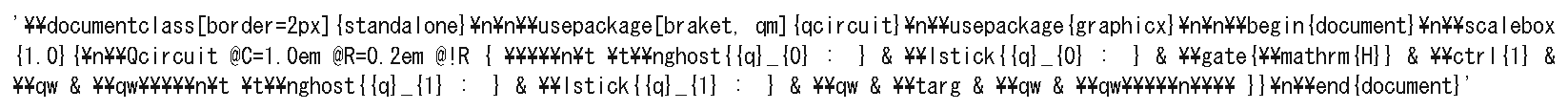
  1. qc.draw(‘mpl’)

  2. qc.draw(‘text’)

  3. print(qc)

  4. qc.draw(‘latex_source’)

答えはこちら

  1. qc.draw(‘latex_source’)

問題29#

以下の結果が表示されるコードは？#

qc = QuantumCircuit(2)

qc.h(0)
qc.cx(0,1)

#insert code 下記選択しから選んでください

問題画像

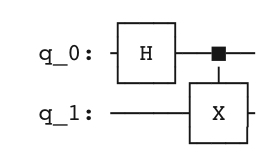
  1. qc.draw(‘mpl’)

  2. qc.draw(‘text’)

  3. print(qc)

  4. qc.draw(‘latex_source’)

答えはこちら

  1. print(qc)

問題30#

以下の結果をPng形式で保存するコードは？#

qc = QuantumCircuit(2)

qc.h(0)
qc.cx(0,1)

#insert code 下記選択しから選んでください

問題画像

  1. qc.draw(‘mpl’, filename=’test.png’)

  2. qc.draw(‘text’, filename=’test.png’)

  3. print(qc, filename=’test.png’)

  4. qc.draw(‘latex_source’, filename=’test.png’)

答えはこちら

  1. qc.draw(‘mpl’, filename=’test.png’)

問題31#

以下のQiskit version情報を表示するコードは？#

問題画像

  1. print(qiskit.qiskit_version)

  3. print(qiskit.version)

答えはこちら

  1. print(qiskit.version)

問題32#

以下のQiskit version情報を表示するコードは？#

問題画像

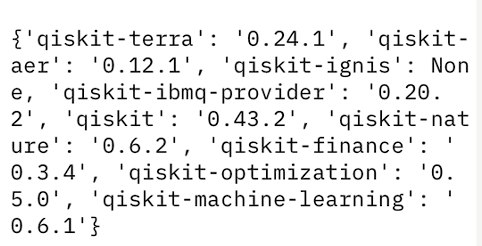
  1. print(qiskit.qiskit_version)

  3. print(qiskit.version)

答えはこちら

  1. print(qiskit.qiskit_version)

問題33#

以下のQiskit version情報を表示するコードは？#

問題画像

  1. print(qiskit.qiskit_version)

  3. print(qiskit.version)

答えはこちら

問題34#

一番早く実行できるマシンはどれか？#

問題画像

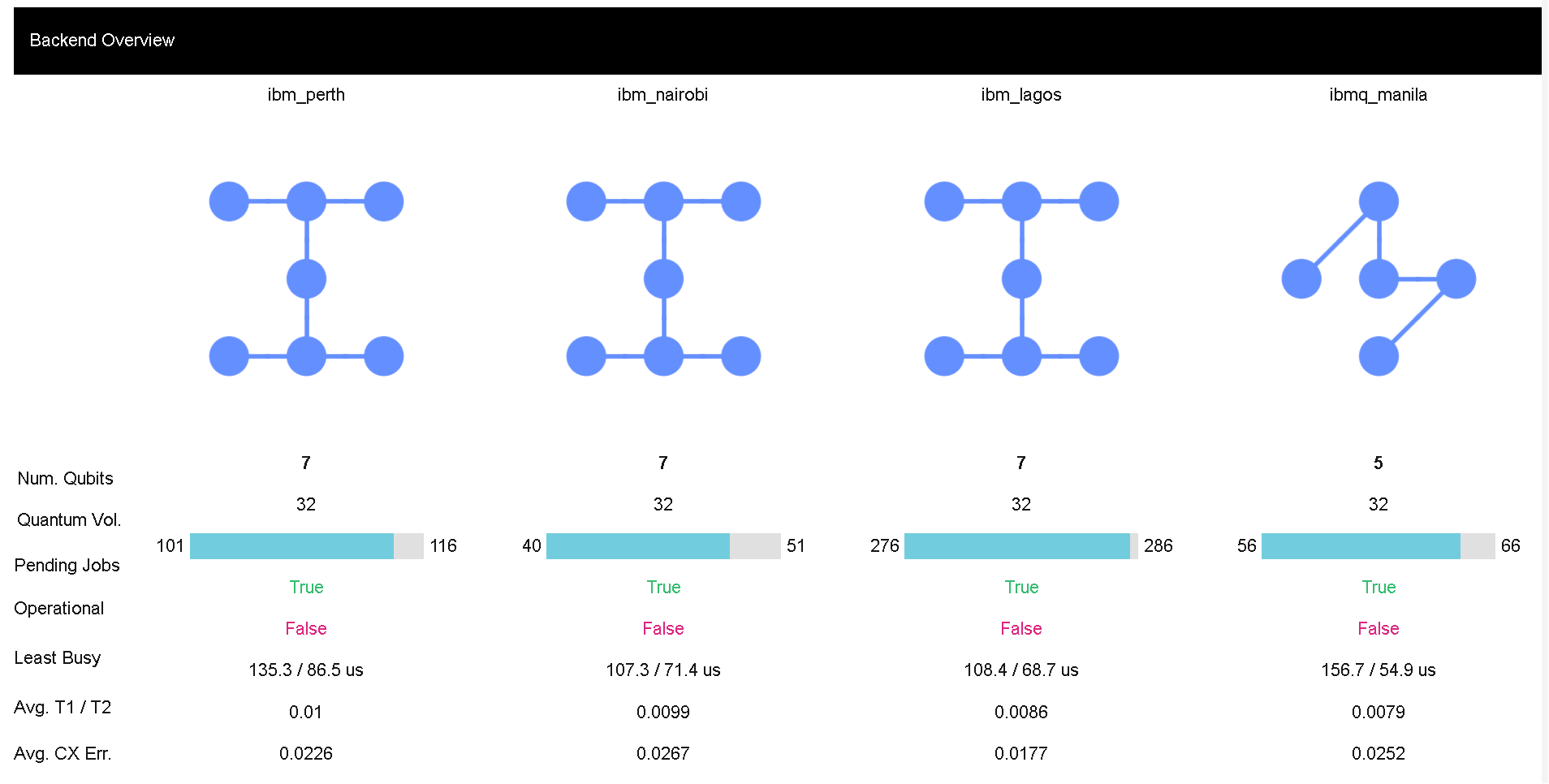
  1. ibm_perth

  2. ibm_nairobi

  3. ibm_lagos

  4. ibmq_manila

答えはこちら

Pending jobsが少ないものを選択します
2. ibm_nairobi

問題35#

誤りが少ない可能性が高いのは？#

問題画像

  1. ibm_perth

  2. ibm_nairobi

  3. ibm_lagos 4．ibmq_manila

答えはこちら

コヒーレンス時間のながさをAvg T1/t2で確認

  1. ibm_perth

問題36#

単一量子ビットゲートを分解するコードは？#

  1. qc.converts

  2. qc.traspiler

  3. qc.decompose

  4. qc.operators

答えはこちら

問題画像

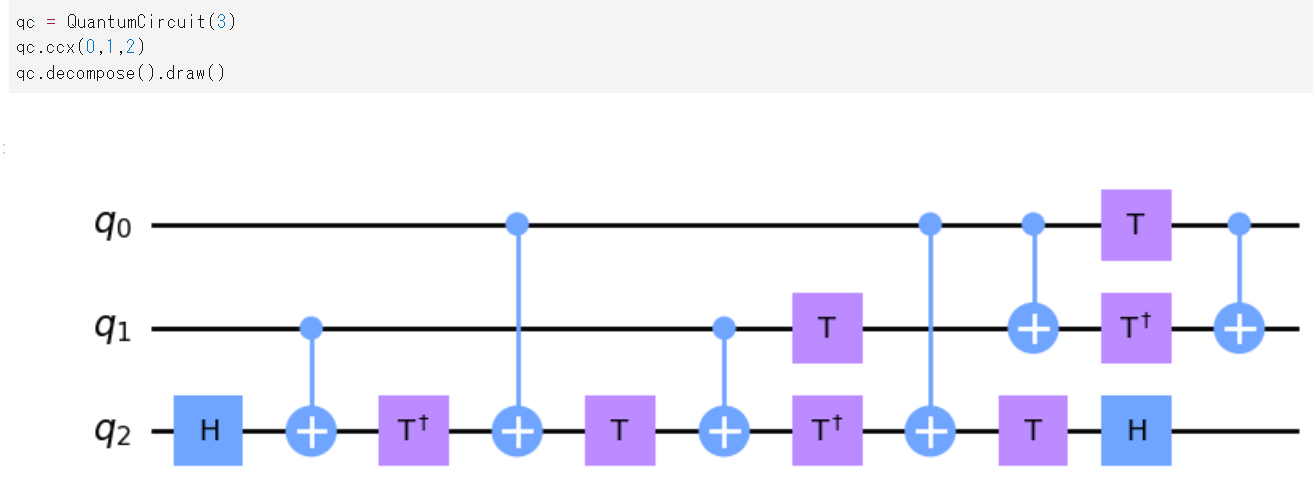
問題37#

下記になるコードは？#

qc = QuantumCircuit(3)
#insert code 下記選択肢から選んでください
qc.draw()

問題画像

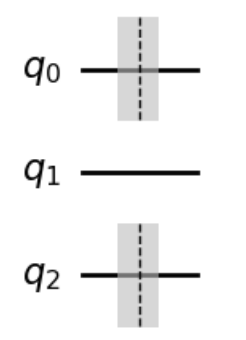
  1. qc.barrier([0,2])

  2. qc.barrier()

  3. qc.barrier(q0,q2)

  4. qc.barrier(0,2)

答えはこちら

  1. qc.barrier([0,2])と

  2. qc.barrier(0,2)

問題38#

量子回路の最適化を行わないためのoptimization_levelは？#

optimization_level()

  1. 0

  2. 1

  3. 2

  4. 3

答えはこちら

  1. 0

問題39#

画像内で赤く囲んだ部分は何ですか？#

問題画像

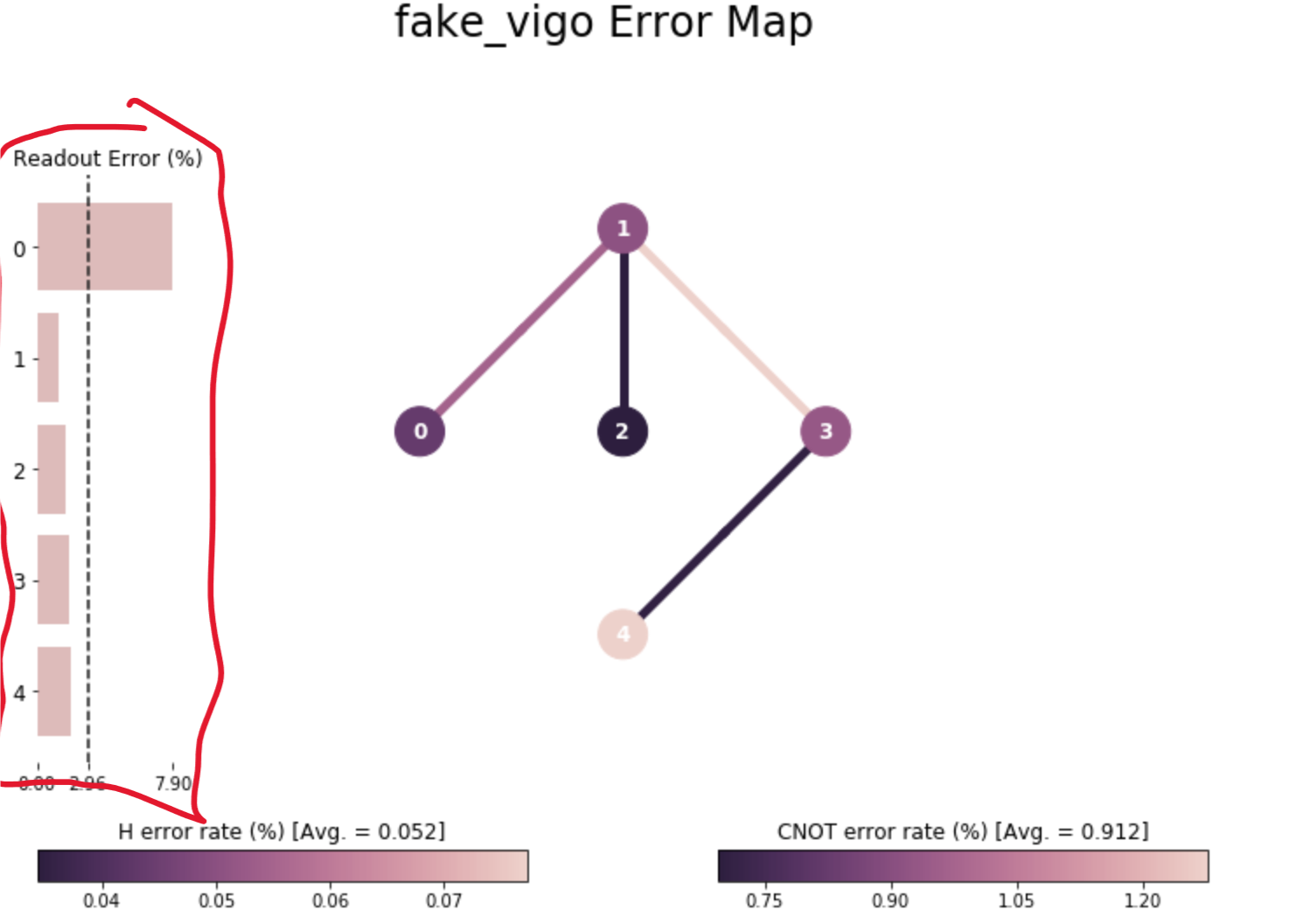
  1. 読み取り時のエラー率

  2. 論理ゲートのエラー率

  3. 物理的なビットの結びつき

答えはこちら

  1. 読み取り時のエラー率

問題40#

画像内で赤く囲んだ部分は何ですか？#

問題画像

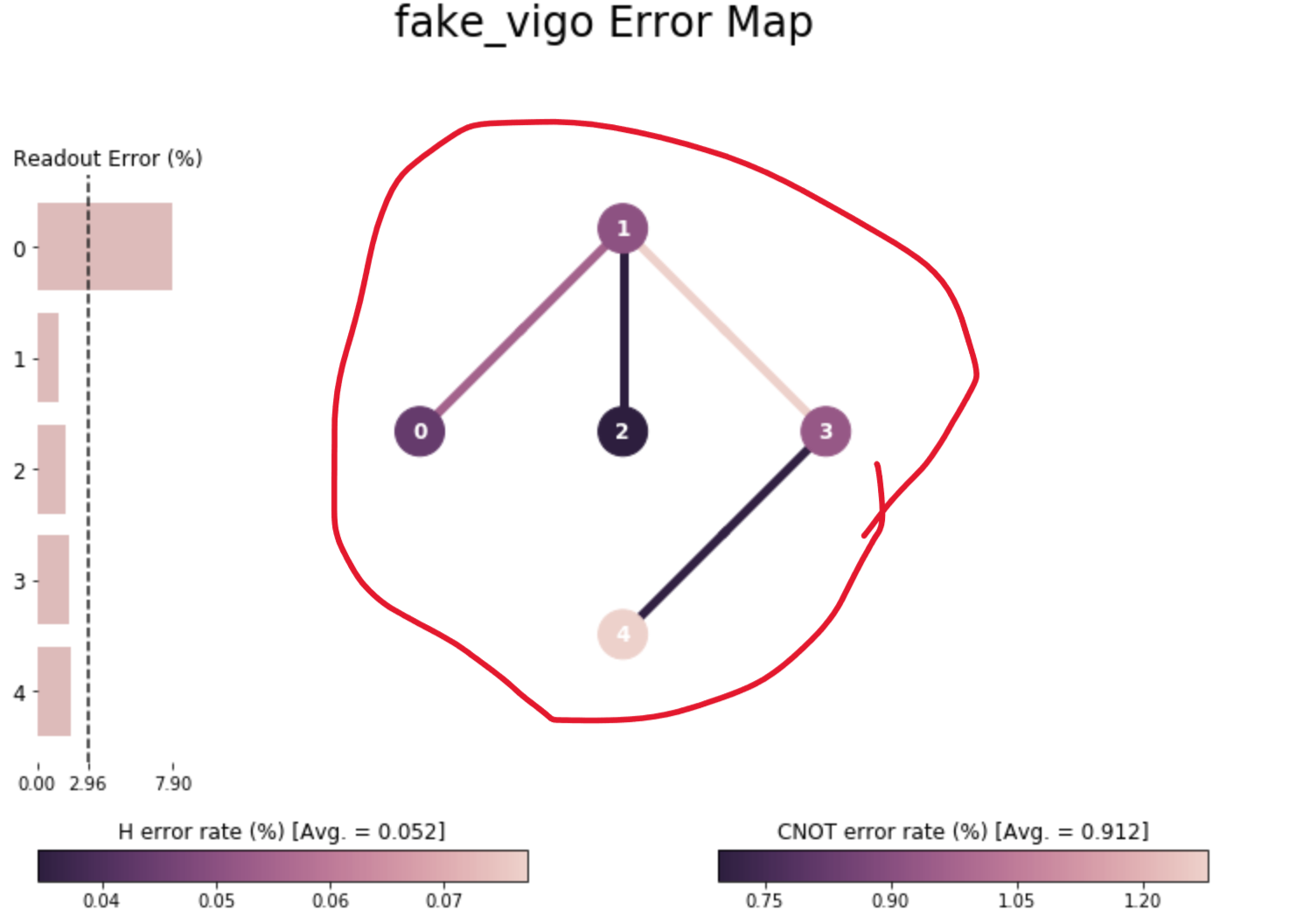
  1. 読み取り時のエラー率

  2. 論理ゲートのエラー率

  3. 物理的なビットの結びつき

答えはこちら

  1. 論理ゲートのエラー率

問題41#

画像内で赤く囲んだ部分は何ですか？#

問題画像

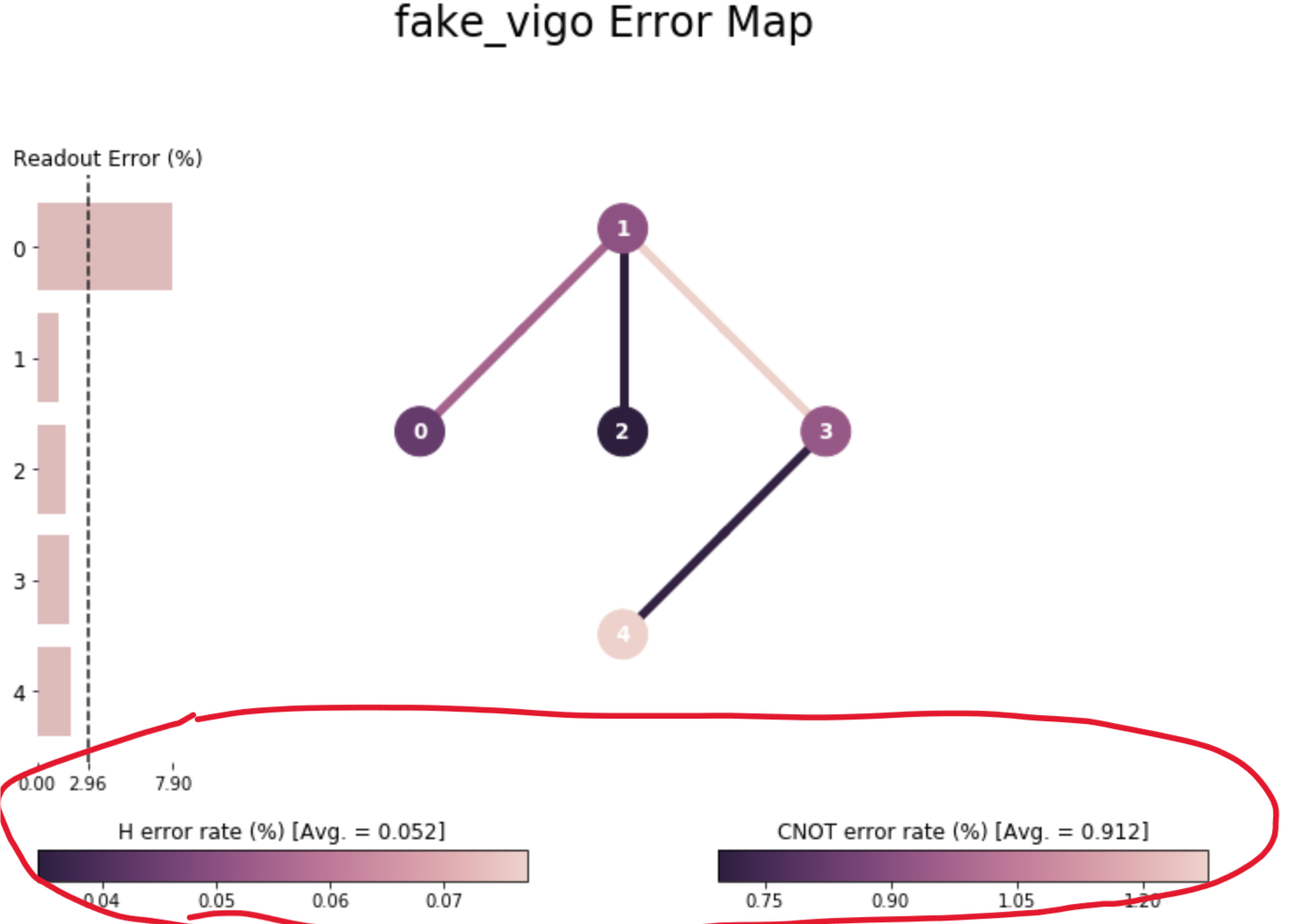
  1. 読み取り時のエラー率

  2. 論理ゲートのエラー率

  3. 物理的なビットの結びつき

答えはこちら

  1. 物理的なビットの結びつき

問題42#

電子回路をシミュレーションするパッケージで、BasicAerにふくまれるもののうち、複素ベクトルである量子状態を返すのはどれか？#

  1. qasm_simulator

  2. statevector_simulator

  3. unitary_simulator

答えはこちら

  1. statevector_simulator

問題43#

電子回路をシミュレーションするパッケージで、BasicAerにふくまれるもののうち、複素ベクトルである量子状態を返すのはどれか？#

  1. qasm_simulator

  2. statevector_simulator

  3. unitary_simulator

答えはこちら

  1. statevector_simulator

問題44#

電子回路をシミュレーションするパッケージで、BasicAerにふくまれるもののうち、ユニタリー演算で利用するものは？#

  1. qasm_simulator

  2. statevector_simulator

  3. unitary_simulator

答えはこちら

  1. unitary_simulator

問題45#

２つの量子状態の類似性を計算するもので、２つの状態ベクトルから計算するのは？#

  1. state_fidelity()

  2. process_fidelity()

  3. average_gate_simulator

答えはこちら

  1. state_fidelity()

問題46#

、２つのオペレータ間の類似性を計算するもので、２つのユニタリ行列の近さを表わすのは？#

  1. state_fidelity()

  2. process_fidelity()

  3. average_gate_simulator

答えはこちら

  1. process_fidelity()

問題47#

量子チャネルとオペレータ、あるいは２つのオペレータ間の類似性を計算するものだが、 （に等しい#

  1. state_fidelity()

  2. process_fidelity()

  3. average_gate_simulator

答えはこちら

  1. average_gate_simulator

両者のprocess_fidelity×次元数＋１）/（ 次元数＋１）に等しい

問題48#

state_fidelity()、process_fidelity()は類似性が高いと数字はどうなるか？#

  1. 0

  2. 0.5

  3. 1

  4. 10

答えはこちら

  1. 1 類似性がたかいと１に近づきます

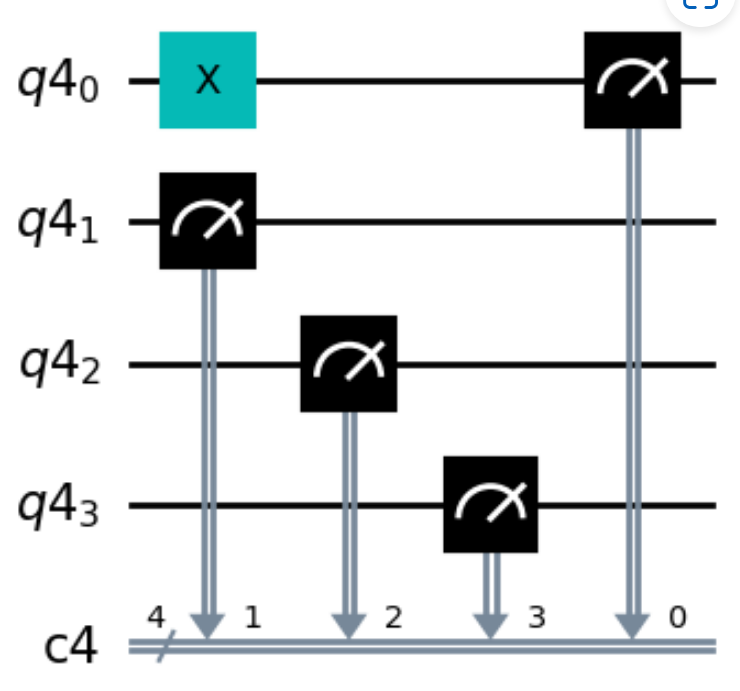
問題49#

以下のコードで得られるのは？#

qr = QuantumRegister(4)
cr = ClassicalRegister(4)
qc=QuantumCircuit(qr, cr)
qc.x(0)
qc.measure(qr[0:5],cr[0:5])

simulator = BasicAer.get_backend(‘qasm_simulator’)
result = execute(qc, simulator).result()
counts = result.get_counts(qc)
print(counts)

  1. {‘1000’: 1024}

  2. {‘0100’: 1024}

  3. {‘0010’: 1024}

  4. {‘0001’: 1024}

答えはこちら

  1. {‘0001’: 1024}

問題画像

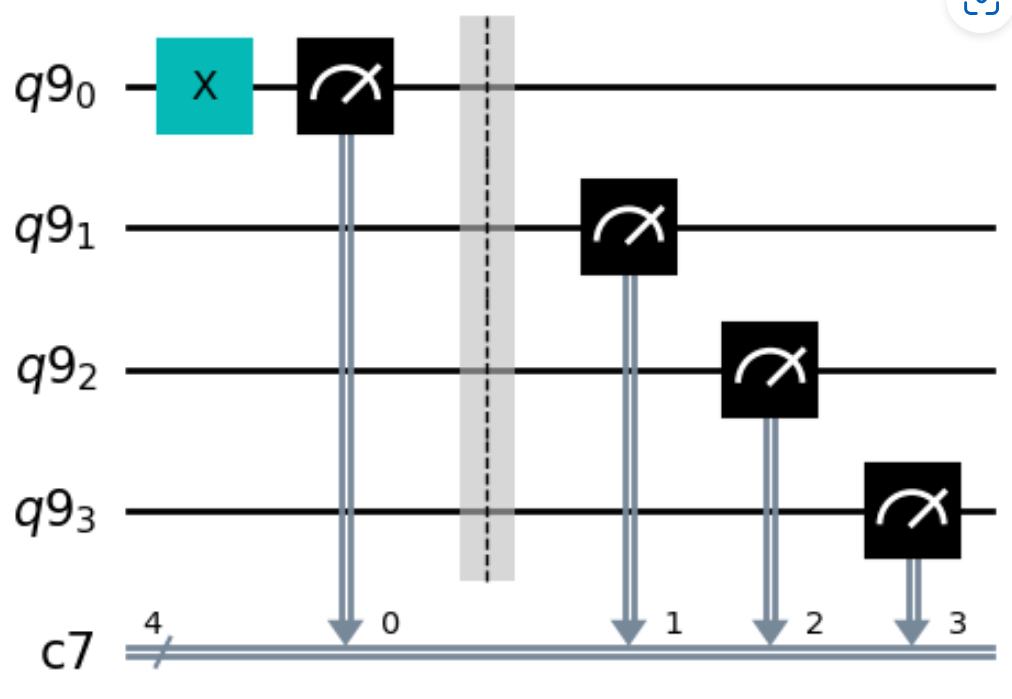
問題50#

以下のコードで得られるのは？#

qr = QuantumRegister(4)
cr = ClassicalRegister(4)
qc=QuantumCircuit(qr, cr)
qc.x(0)
qc.measure(qr[0],cr[0])
qc.barrier()
qc.measure(qr[1:4],cr[1:4])

simulator = BasicAer.get_backend(‘qasm_simulator’)
result = execute(qc, simulator).result()
counts = result.get_counts(qc)
print(counts)

  1. {‘1000’: 1024}

  2. {‘0100’: 1024}

  3. {‘0010’: 1024}

  4. {‘0001’: 1024}

答えはこちら

  1. {‘0001’: 1024}

問題画像

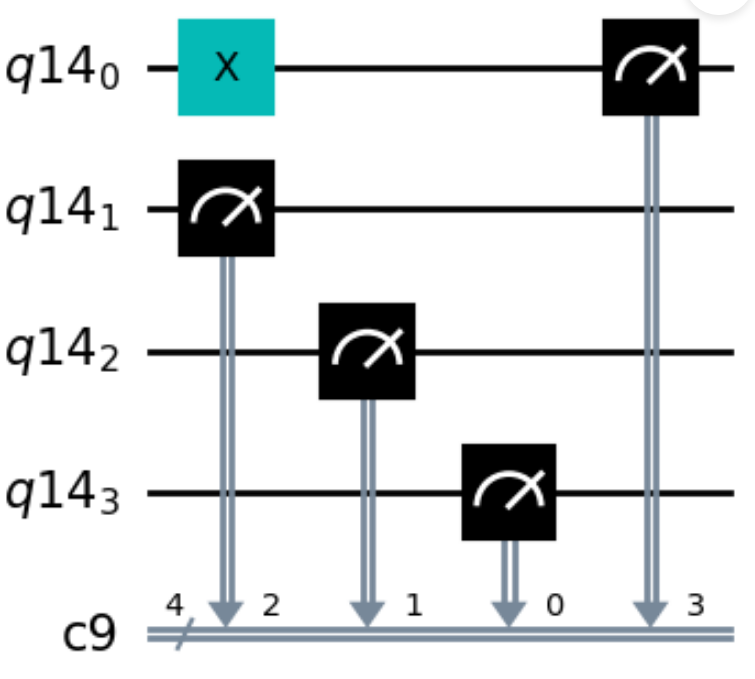
問題51#

以下のコードで得られるのは？#

qr = QuantumRegister(4)
cr = ClassicalRegister(4)
qc=QuantumCircuit(qr, cr)
qc.x(0)
qc.measure(qr[0],cr[3])
qc.measure(qr[1],cr[2])
qc.measure(qr[2],cr[1])
qc.measure(qr[3],cr[0])
qc.draw(‘mpl’)
simulator = BasicAer.get_backend(‘qasm_simulator’)
result = execute(qc, simulator).result()
counts = result.get_counts(qc)
print(counts)

  1. {‘1000’: 1024}

  2. {‘0100’: 1024}

  3. {‘0010’: 1024}

  4. {‘0001’: 1024}

答えはこちら

  1. {‘1000’: 1024}

問題画像

以下テンプレート 改行は#

問題??#

問題文text#

答えはこちら

回答text